Six balises méthodologiques pour réussir l’entrée en mathématique

Ce qui me guide dans cet article, c’est la construction de l’abstraction qui nécessite d’être attentif à un certain nombre de balises que je vais présenter et illustrer par des exemples liés à l’apprentissage des nombres entiers naturels.

Ces balises, au nombre de six, ne remplacent pas une orientation pédagogique (pédagogies actives, socioconstructivisme, pédagogie par objectifs…) mais constituent des points d’attention en vue d’assurer l’apprentissage à tous au-delà de la pédagogie choisie.

Balise 1 : Partir du terrain de l’apprenant sans y camper

La première étape incontournable d’un apprentissage signifiant pour les apprenants est de s’appuyer sur l’environnement dans lequel ils vivent, les questions qu’ils se posent à propos de cet environnement, ainsi que le langage qu’ils utilisent pour en parler. Le défi essentiel d’un formateur est d’enseigner les mathématiques en s’appuyant sur des situations qui vont éveiller le questionnement et titiller le désir d’apprendre. Les questions vont ensuite se transformer en objets de recherche et d’apprentissage, et conduire à l’élaboration de savoirs et de savoir-faire qui seront réinvestis dans de nouvelles situations.

Les portes d’entrée qui vont donner du sens à l’apprentissage des mathématiques sont multiples. Il peut s’agir de :

• situations directement liées à la vie du groupe : effectifs du groupe et du centre de formation, absents et présents, sorties…
• situations de la vie quotidienne : achats, factures, mesures, recettes…
• questions d’actualité : sondages, démographie, évènements…
• questions purement didactiques qui peuvent éveiller la curiosité : est-ce que ces deux quantités sont égales ? comment faire pour partager en trois parts égales ? …

Dans l’introduction d’un des rares livres relatifs aux mathématiques écrits dans les premières années de développement de l’alphabétisation des adultes¹, on peut lire les recommandations suivantes : « Un adulte est motivé par la résolution de problèmes qu’il peut rencontrer mais cela ne veut pas dire qu’il faut se limiter aux achats, au bricolage et à la cuisine. Notre objectif n’est pas prioritairement de résoudre des problèmes concrets mais de permettre aux apprenants de maitriser des outils mathématiques grâce auxquels ils pourront comprendre des situations multiples. Ce n’est donc pas très important de savoir si on rencontre le problème dans ces termes. Les problèmes sont choisis parce qu’à partir de ceux-ci, il y a moyen d’acquérir une notion fondamentale. On cherche à sortir du problème pour en saisir la généralité. »

Balise 2 : S’appuyer sur du matériel et apprendre à s’en passer

Pour entrer dans l’analyse d’une situation au-delà de la compréhension de la langue et des mots utilisés pour la décrire, il faut que chacun puisse s’en faire une représentation. C’est à ce stade que la mise à disposition d’un matériel didactique est importante.

Ainsi pour se représenter des collections données, on peut disposer :

• soit d’un matériel non organisé, par exemple :

• soit d’un matériel organisé :

S’il s’agit de positionner des nombres, on peut utiliser des supports structurés comme :

• une file des nombres :

• un tableau de 100 :

L’utilisation de ce matériel permet de décontextualiser progressivement les situations afin d’en avoir une représentation centrée sur les quantités ou les positions, ainsi que les relations entre elles. L’utilisation d’un matériel n’est pas le fruit du hasard mais doit être choisi en fonction de l’apprentissage visé. Par ailleurs, l’usage et la manipulation d’un matériel ne sont pas un but en soi. Ils servent d’intermédiaire entre la réalité et la pensée. Il est donc tout aussi important d’apprendre à s’en passer. À cet effet, l’enjeu est de passer progressivement du geste physique au geste mental.

Voici deux techniques pour apprendre à s’en passer :

• ne donner accès à du matériel que si l’apprenant peut nommer celui qu’il veut utiliser et l’usage qu’il veut en faire (il faut néanmoins tenir compte du fait que certains apprenants n’ont pas accès au vocabulaire requis en raison de leur mécon-naissance du français) ;
• inviter l’apprenant à voir le matériel et son utilisation dans sa tête plutôt que de l’utiliser.

Une étape intermédiaire utile pour y arriver est d’inviter les apprenants à garder des traces de l’utilisation du matériel dans une situation donnée à l’aide d’un dessin.

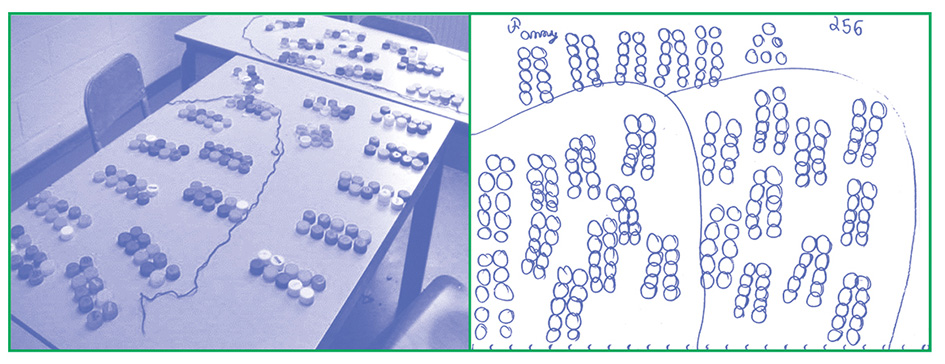
Balise 3 : Schématiser pour catégoriser et modéliser

Au-delà de la manipulation qui permet de comprendre ce qui se passe dans une situation, une étape importante pour accéder aux savoirs mathématiques est la schématisation des situations. Il faut bien distinguer les schémas des dessins. En effet, un dessin, au sens artistique du terme, n’aide pas nécessairement à se représenter une situation avec des lunettes mathématiques. La fonction d’un schéma est de désencombrer la situation en se centrant, par exemple, sur les nombres et les relations entre eux, indépendamment du contexte.

Les premiers schémas auxquels il importe de familiariser les apprenants sont les schèmes des nombres dont voici un exemple pour représenter les nombres de 1 à 10 :

La structure des schèmes des nombres est essentielle et doit être choisie de façon à mettre en évidence certaines propriétés des nombres jugées essentielles en vue du calcul. Les propriétés des nombres qui apparaissent dans la présentation ci-dessus sont les suivantes :

• les schèmes de 6 à 10 sont décomposés à partir de 5 : par exemple, 6, c’est 5 et 1 ; 7, c’est 5 et 2 ;
• les compléments à 5 pour les nombres en dessous de 5 sont visibles : par exemple, pour aller de 3 à 5, il manque 2 ;
• les compléments à 10 pour les nombres supérieurs ou égaux à 5 sont visibles : par exemple, il manque 3 à 7 pour avoir 10.

Dans le domaine des opérations, il est également intéressant de passer par des schémas pour traduire des situations et conduire à l’élaboration de catégories de situations qui se ressemblent dans la mesure où elles s’appuient sur des schémas semblables. Cela permet de relier des situations ou des phénomènes entre eux par la relation « c’est comme… ». C’est un processus essentiel pour identifier différents sens des opérations à travers les situations rencontrées ou encore pour classer des stratégies de calcul.

À titre d’exemple, dans le tableau ci-après, nous présentons deux catégories de sens de la soustraction auxquelles correspondent deux schémas distincts.

Balise 4 : Construire les images mentales et les mettre en mémoire

Tant l’utilisation d’un matériel adéquat que la schématisation des situations contribuent à l’élaboration d’images mentales liées aux notions abordées, c’est-à-dire des représentations qu’on se fait dans sa tête sans plus avoir recours à un support matériel. Pour qu’elles soient efficaces, ces images mentales doivent rendre compte des propriétés essentielles et utiles des concepts.

À titre d’exemple, nous présentons ci-dessous les supports aux images mentales de la numération dont l’enjeu essentiel est de percevoir la répétition des groupements par dix. Nous présentons
ce phénomène avec deux sortes de matériel différent :

C’est en répétant plusieurs fois une activité de dénombrement de grandes collections (de l’ordre de plusieurs centaines) par groupements de 10 qu’on inscrira progressivement ce type de structure dans la tête des apprenants.

Balise 5 : Verbaliser, expliciter les objectifs visés

Avant d’être écrites, les mathématiques se vivent et se parlent. Le langage oral, tant celui des apprenants que celui du formateur, joue un rôle essentiel dans ce travail de compréhension et d’abstraction. La verbalisation par les apprenants de leurs démarches et de leurs observations contribue à la construction des savoirs. Le rôle du formateur est d’inviter et aider régulièrement les apprenants à mettre des mots sur ce qui se passe. Il s’agit de développer le vocabulaire nécessaire à cette verbalisation, dont voici quelques exemples :

• pour comparer des quantités : plus que, moins que, autant que, c’est pareil, il manque…
• pour comparer des positions : devant, derrière, avant, après, plus loin…
• pour agir sur les quantités : ajouter, réunir, rassembler, enlever, constituer des parts égales ou inégales…
• pour agir sur les positions : reculer, avancer, dépasser…

Il est vraiment important dans des groupes d’alphabétisation d’intégrer l’apprentissage de la langue à celui des mathématiques².

Par ailleurs, si on veut que ce travail de construction des savoirs permette à tous d’apprendre, il est indispensable d’expliciter systématiquement les objectifs visés et de mettre des mots sur ce qui se passe à toutes les étapes. Par ses interventions explicites, le formateur invite les apprenants à porter leur attention sur la construction des savoirs et savoir-faire visés.

Voici un exemple :

• « Nous allons travailler les doubles. Vous savez tous déjà que ‘un et un, ça fait deux’ ; ‘deux et deux, ça fait quatre’, etc.
• On peut obtenir facilement les cinq premiers doubles avec ses mains en vis-à-vis et les cinq suivants avec les mains de deux personnes en vis-à-vis, comme ceci :

• Chacun va noter tous les doubles qu’il connait déjà. On va essayer d’aller plus loin et d’en connaitre plus car on sait que quand on a des calculs faciles en tête, ça peut nous aider pour faire des calculs plus difficiles. »

Balise 6 : Identifier les acquis et les structurer

Au-delà de l’explicitation des objectifs et des démarches, il est essentiel, au terme du travail, de distinguer l’apprendre du faire et de vérifier s’il y a eu apprentissage. Ce passage de l’activité aux savoirs doit être explicite si on veut s’assurer que les apprenants, au départ éloignés de la culture scolaire, perçoivent que, derrière les actions réalisées, il y a des savoirs et des savoir-faire mobilisables. Pour y arriver, il ne suffit pas de poser la question « qu’est-ce qu’on a appris ? », mais bien de mettre en place une véritable méthodologie adaptée au niveau des apprenants, qui invite chacun à refaire le parcours vécu pour en extraire les enjeux essentiels. Ensuite, on confronte les apprentissages des uns et des autres afin de constituer un savoir commun qu’on va nommer et organiser sous forme de référentiels collectifs.

En reprenant l’exemple du travail sur les doubles décrits à la balise 5, on peut, dans un référentiel portant sur les nombres et les opérations, structurer les acquis de la façon suivante :

Conclusion

Comme vous aurez pu le constater, les exemples proposés dans cet article sont tous issus de l’apprentissage des nombres naturels et des opérations. Toutefois, les balises présentées restent valables dans d’autres domaines des mathématiques comme les grandeurs (longueurs, aires, volumes, masses…) et leurs mesures, les fractions, les figures géométriques…

Quel que soit le domaine d’application, les six balises que nous venons de décrire s’articulent les unes aux autres et forment un tout. Il ne peut être question d’en privilégier une au détriment d’une autre. Elles constituent différentes portes pour faire entrer les apprenants dans les mathématiques, non pas celles qui se réduisent à quelques techniques, voire à quelques trucs, mais
celles qui aident à penser le monde.

L’article ci-dessus s’appuie sur le livre d’Anne Chevalier :

Réussir l’entrée en mathématiques. Construire les nombres naturels et les opérations, Couleur livres, 2020.

Ce livre donne des repères aux enseignants de l’école fondamentale et aux formateurs en alphabétisation pour faire entrer tous les apprenants dans l’univers des nombres en proposant cinq fils conducteurs à parcourir : construire les premiers nombres, comprendre la numération, appréhender l’ordre des nombres, donner du sens aux opérations, développer des stratégies
de calcul.

Les six balises méthodologiques développées dans cet article sont présentées dans l’introduction du livre et illustrées pour chacun de ces fils conducteurs.

1. Michel TISSIER (coord.), Calcul et raisonnement mathématique. Formation de base en mathématiques pour adultes, CLAP, Paris, 1979 (épuisé mais disponible en prêt au Centre de documentation du Collectif Alpha).                 
2. À ce propos, lire : Anne CHEVALIER, De la numération orale à la numération écrite, un pas difficile à franchir, in Journal de l’alpha, n°211, 4^e trimestre 2018, pp. 88-95, www.lire-et-
   ecrire.be/ja211